入試をはさみ、しばらくぶりの数学者の時間。前回の「ロープにつながれたヒツジ」問題の特徴をつかって、自分でも問題をつくった。
数学者の時間 特殊化(ためす)から問題解決を
数学者の時間 特殊化(ためす)から問題解決を
この「ロープにつながれたヒツジ」問題の特徴は「欠けた円の面積を求める」「いくつかの面積が複合している」。つまり、この二つの要素をつかって問題づくりができていればOK。
この時間は、前回の良問である「ロープにつながれたヒツジ」問題を解いてもOK、また、今回のミニ・レッスン「問題の特徴をいかす」で紹介した子どものつくった「ロープにつながれた友だち」問題をといてもOK。これもまたシンプルにいい問題。
「右の図のような一辺が10mの家があります。そこに○○さんと□□さんが10mの糸につながれています。○○さんはAに、□□さんはBにつながれています。2人が動ける範囲の重なりは何㎡ですか。」
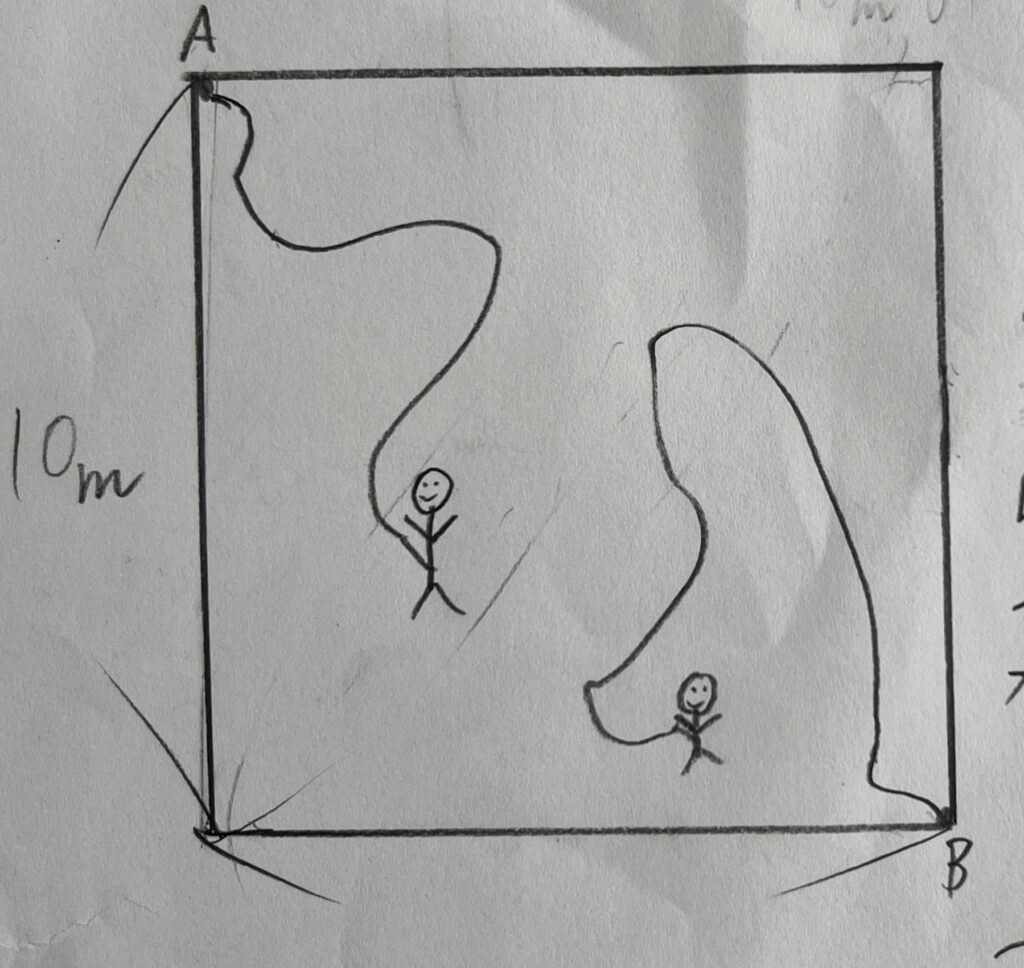
毎回のミニ・レッスンにはこうやって子どもたちがつくった問題を使っている。今回は、前回のヒツジ問題をすでにといて自分で問題づくりをしていた子の問題をかりた。この問題は修正する前は、「2人が刑務所に鎖でつながっている問題」だったので、それはさすがに、、、と修正を依頼してこうなった。
となりのクラスでは、おもしろい問題をつくっている子がいた。じつはこれってかなり頭を使う問題になっている。凸凹のところのロープの曲がり具合がまた頭をひねるつくりになっている。これも問題の特徴をいかしたよい問題のひとつ。
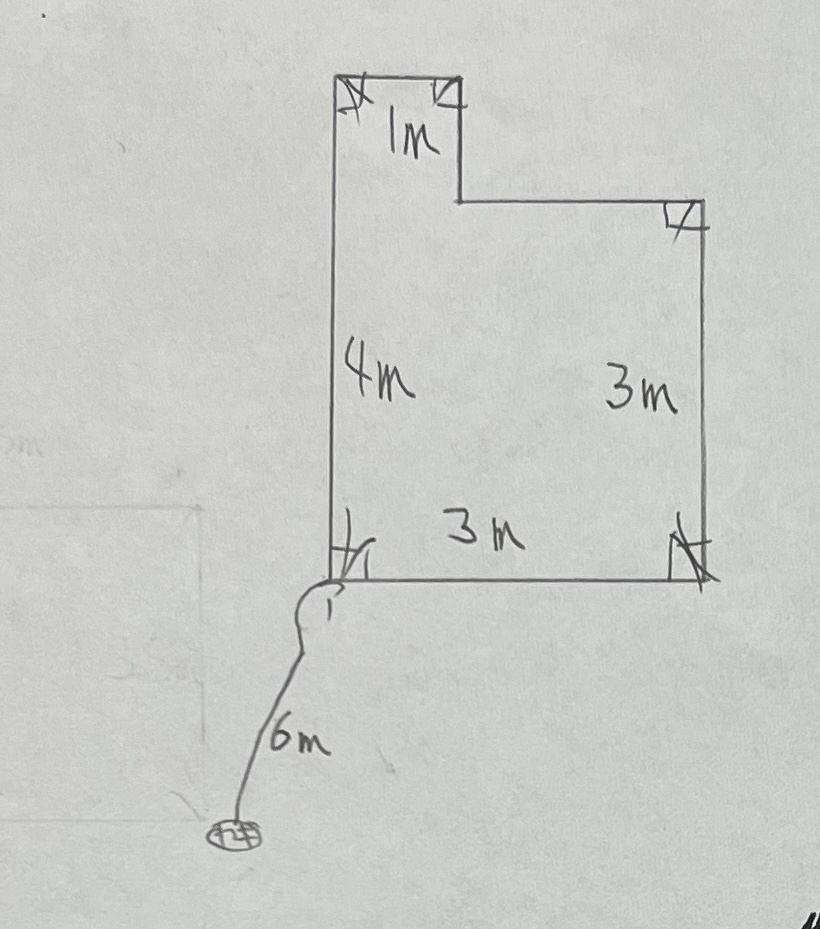
さらには、頂点Aの転がった弧の長さを問う問題。ロープの自由な動きから三角形を回転させる動きへと発想を広げ、さらには面積から円周に拡張。なかなかやるな。

数学者の時間は、子どもたちの可能性がまた一歩大きく広がる時間。次回は、子どもたちが作った問題を解き合う時間へ。